|
FOURIER TRANSFORM
Overview
Fourier Transforms were originally developed as an engineering tool to study repetitious
phenomena such as the vibration of a stringed musical instrument or an airplane wing during
flight. It is used in technical analysis to detect cyclical patterns within prices.
It is beyond the scope of this book to provide a full explanation of Fourier analysis.
Further information can be found in "Technical Analysis of Stocks and Commodities" (TASC),
Volume One issues #2, #4, and #7; Volume Two issue #4; Volume Three issues #2 and #7
(Understanding Cycles); Volume Four issue #6; Volume Five issues #3 (In Search of the Cause
of Cycles) and #5 (Cycles and Chart Patterns); and Volume Six issue #11 (Cycles).
The complete Fourier analysis concept is called spectral analysis. Fast Fourier
Transform ("FFT") is an abbreviated calculation that can be computed in a fraction of the
time. FFT sacrifices phase relationships and concentrates only on cycle length and
amplitude.
The benefit of FFT is its ability to extract the predominate cycle(s) from a series of
data (e.g., an indicator or a security's price).
FFTs are based on the principal that any finite, time-ordered set of data can be
approximated by decomposing the data into a set of sine waves. Each sine wave has a
specific cycle length, amplitude, and phase relationship to the other sine waves.
A difficulty occurs when applying FFT analysis to security prices, because FFTs were
designed to be applied to non-trending, periodic data. The fact that security prices are
often trending is overcome by "detrending" the data using either a linear regression
trendline or a moving average. To adjust for the fact that security data is not truly
periodic, since securities are not traded on weekends and some holidays, the prices are
passed through a smoothing function called a "hamming window."
Interpretation
As stated above, it is beyond the scope of this book to provide complete interpretation of
FFT analysis. I will focus my discussion on the "Interpreted" Fast Fourier Transforms
found in the MetaStock computer program. This indicator shows the three predominate cycle
lengths and the relative strength of each of these cycles.
The following chart displays the
Interpreted FFT of US Steel.
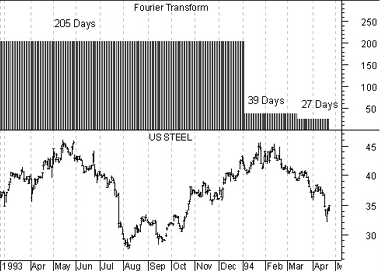 The Interpreted FFT shows that predominate cycle lengths
in US Steel are 205, 39, and 27 trading days.
The Interpreted FFT shows that predominate cycle lengths
in US Steel are 205, 39, and 27 trading days.
The Interpreted FFT indicator always displays the most significant cycle (205 days in
this example) on the left and the least significant cycle (27 days in this example) on the
right. The length of each cycle is determined by the numeric value of the indicator (as
read from the y-axis scales on the sides of the chart).
The longer the indicator remains at a specific value, the more predominate it was in the
data being analyzed. For example, in the above chart, the 205-day cycle is five times
stronger than the 39-day cycle, because the indicator was at 205 for a much longer period
(the fact that 205 is five times greater than 39 is coincidental).
Once you know the predominate cycle length, you can use it as a parameter for other
indicators. For example, if you know that a security has a 35-day cycle, you may want to
plot a 35-day moving average or a 35-day RSI on the security.
|

